1、根据函数y=4*4^x+5*2^x特征,函数可以取全体实数,即定义域为(-∞,+∞)。

2、定义域是指该函数的有效范围,函数y=4*4^x+5*2^x的定义域就是使得这个函数关系式有意义的实数的全体构成的集合。
3、用导数知识,计算函数y=4*4^x+5*2^x的一阶导数,根据导数的符号,判断函数的单调性。

4、导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。
5、 如果函数y=f(x)在区间D内可导(可微),若x∈D时恒有f'(x)>0,则函数y=f(x)在区间D内单调增加;反之,若x∈D时,f'(x)<0,则称函数y=f(x)在区间D内单调减少。
6、通过函数y=4*4^x+5*2^x的二阶导数,判断函数的凸凹性,可知函数在定义域上为凹函数。

7、如果函数f(x)在区间I上二阶可导,则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。
8、解析该y=4*4^x+5*2^x指数和函数在无穷大及原点处的极限。

9、函数五点图,函数y=4*4^x+5*2^x图像上部分点解析表如下:
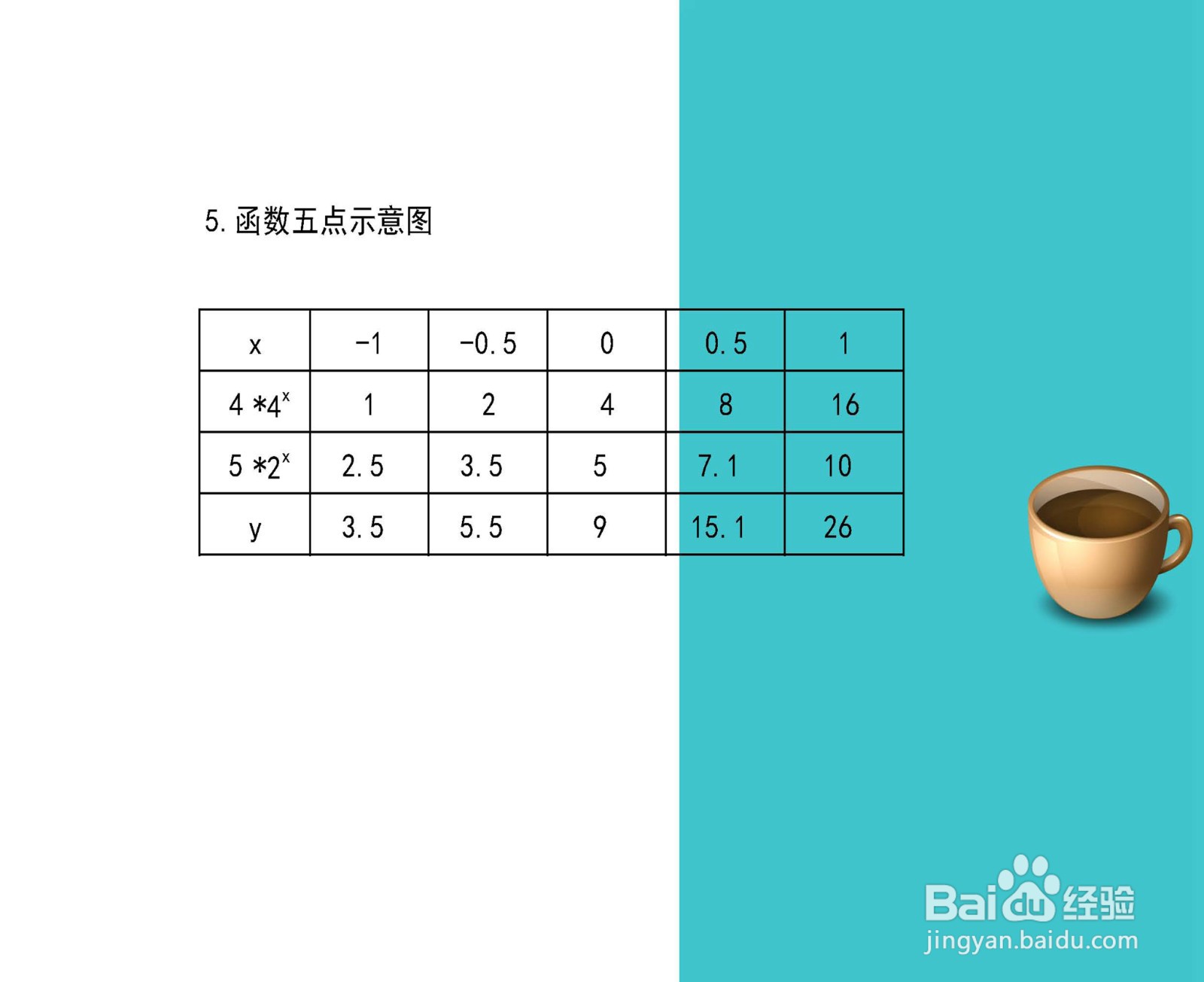
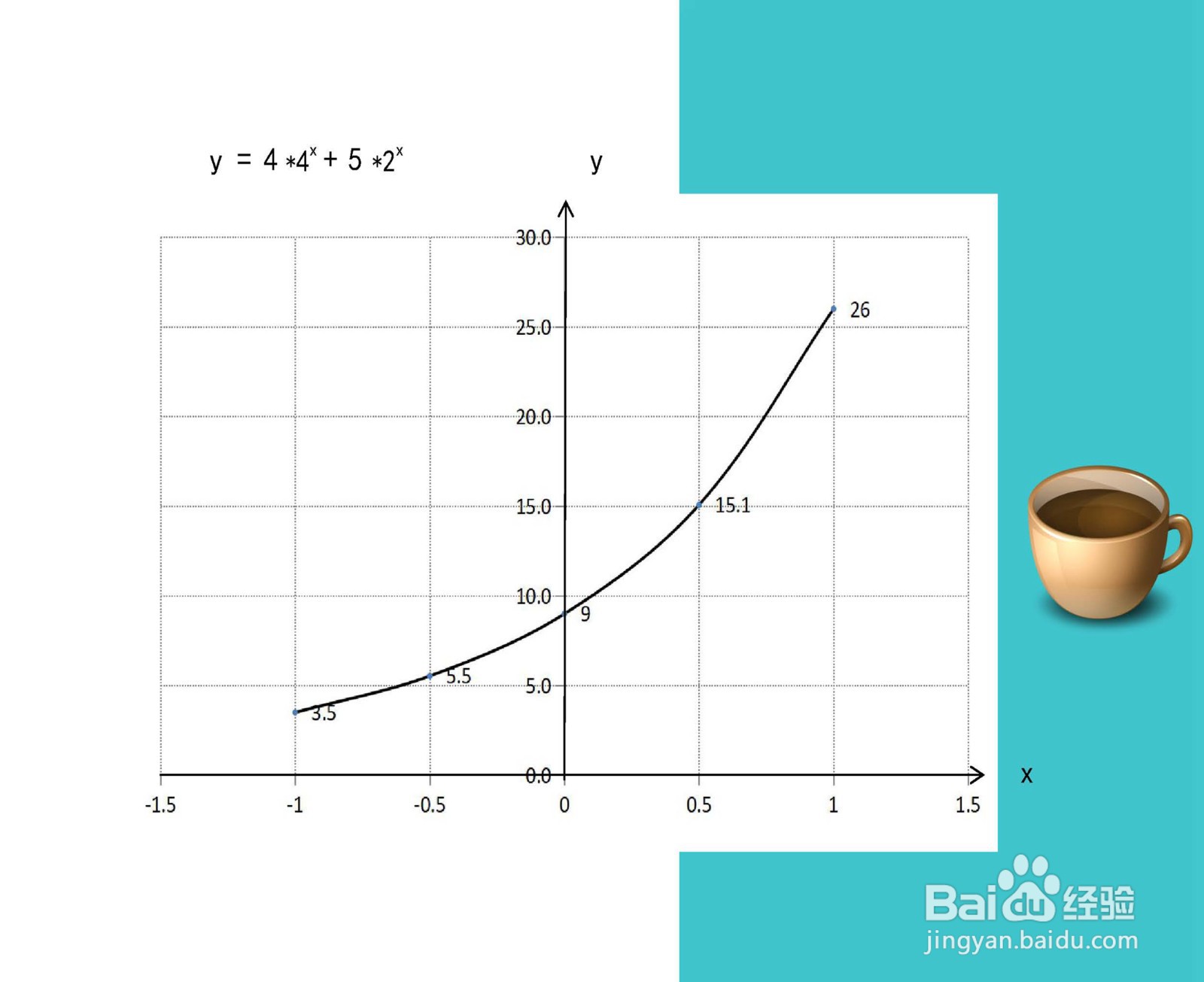
10、综合函数y=4*4^x+5*2^x的定义域、值域、单调性、凸凹性和极限等性质,结合函数的定义域,即可画出函数y=4*4^x+5*2^x的示意图如下: