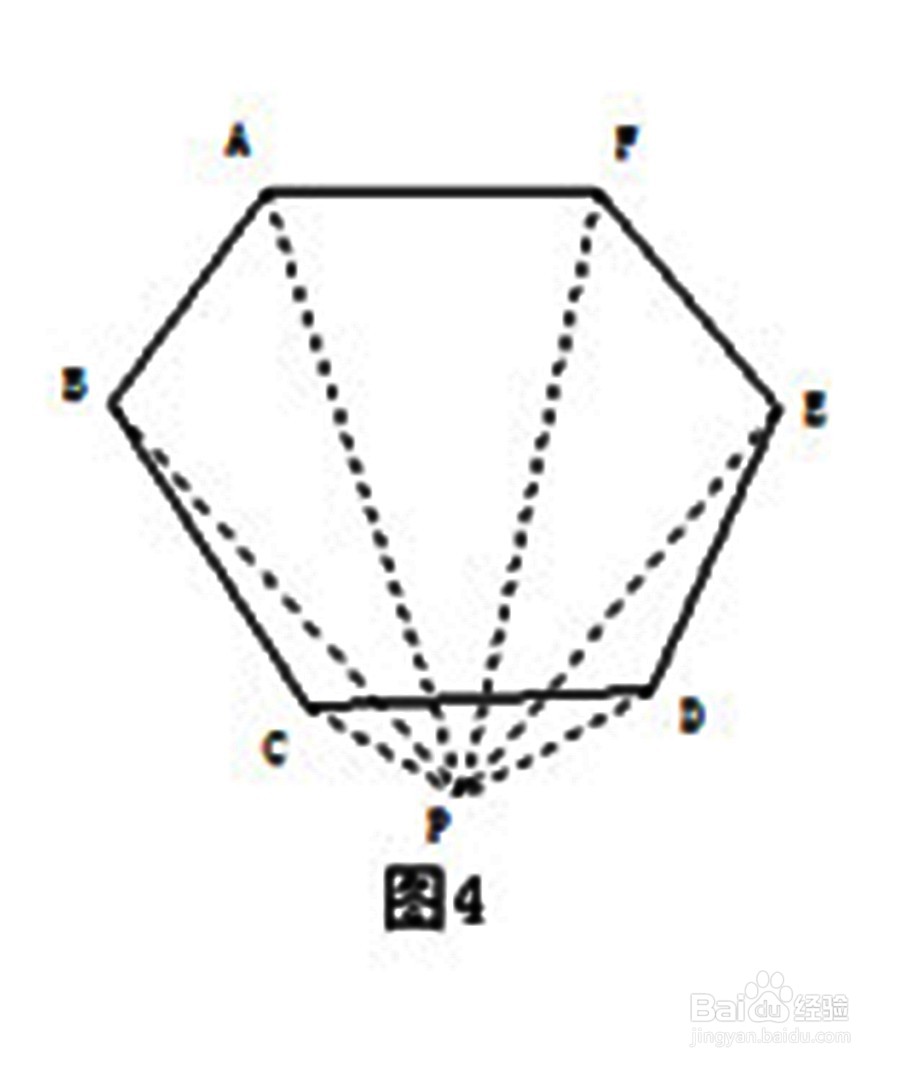
1、方法一:如图1所示,取多边形上任意一个顶点,连接除相邻的两点,则多边形的内角和可转化为三角形内角和之间的关系,即六边形ABCDEF的内角和等于4个三角形内角和之和:4×180°,从而边数为6的多边形内角和为(6-2)×180°=4×180°,再列举其它多边形可以归纳总结出n边形内角和为(n-2)×180° .
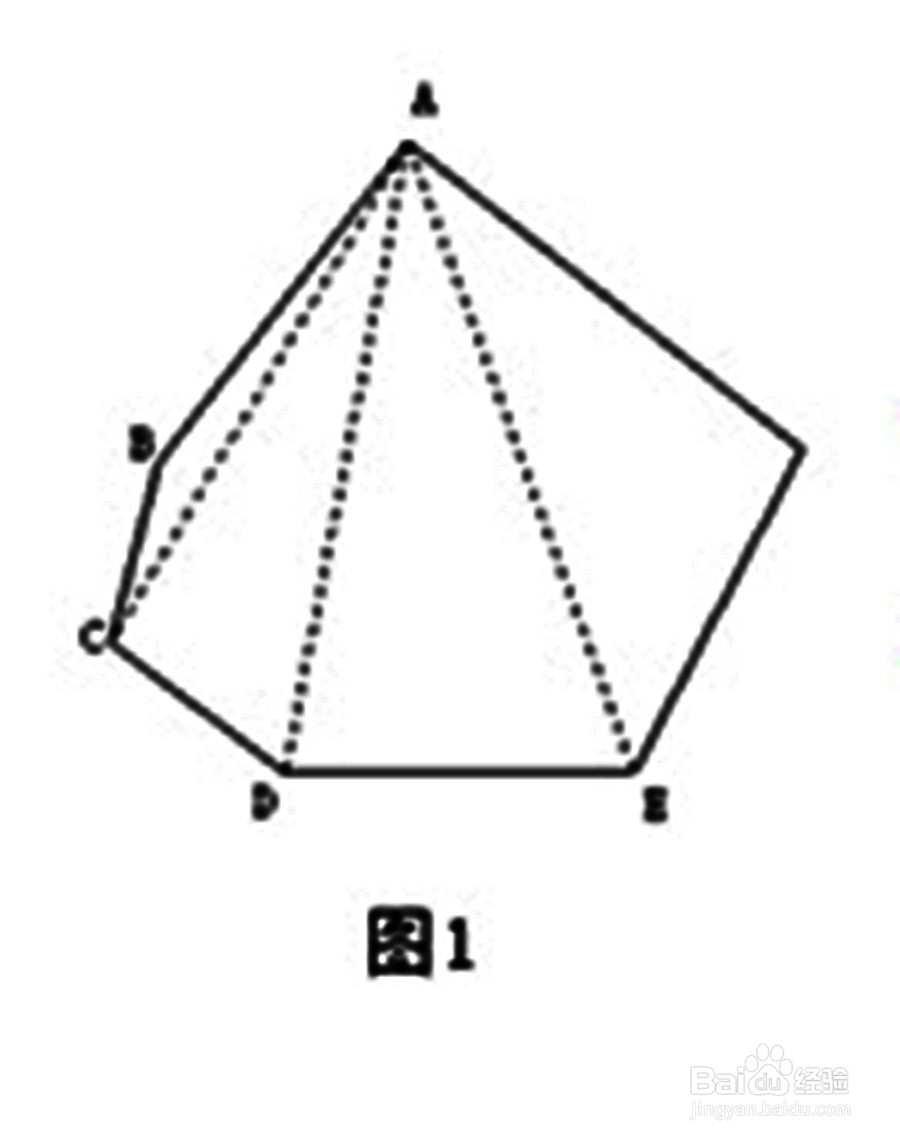
2、方法二:如图2所示,在多边形内任意找一点O,连接各个点,则多边形的内角和可转化为三角形内角和之间的关系,即八边形ABCDEFGH的内角和等于8个三角形内角和减去一个周角的度数:8×180°-360°=8×180°-2×180°=(8-2)×180°,再列举其它多边形可以归纳总结出n边形内角和为(n-2)×180°。
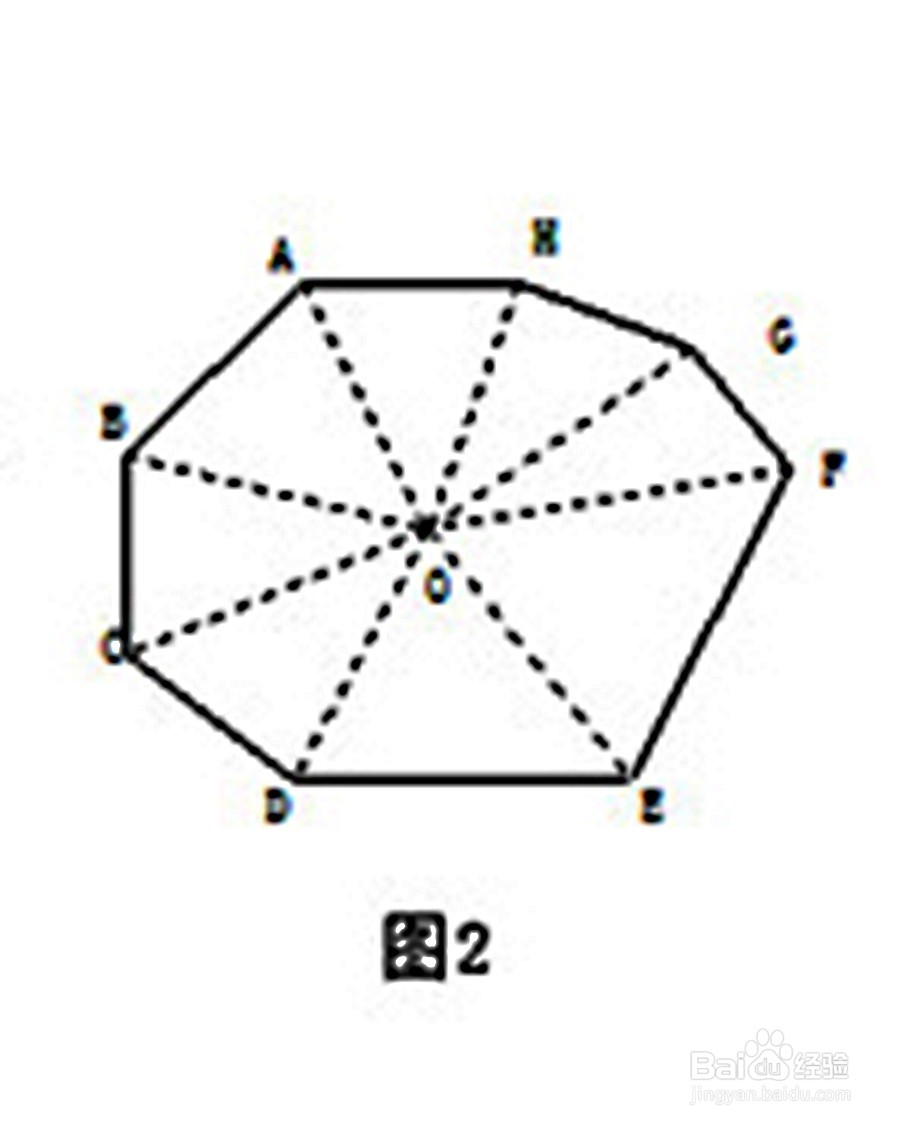
3、方法三:如图3所示,在多边形的一条边上任意取一点P,连接这点与各顶点的线段,把六边形ABCDEF分成了五个三角形,所以此六边形的内角和等于五个三角形的内角和减去一个平角的度数,即:5×180°-180°=4×180°,归纳之后得到n边形的内角和为(n-2)×180°。
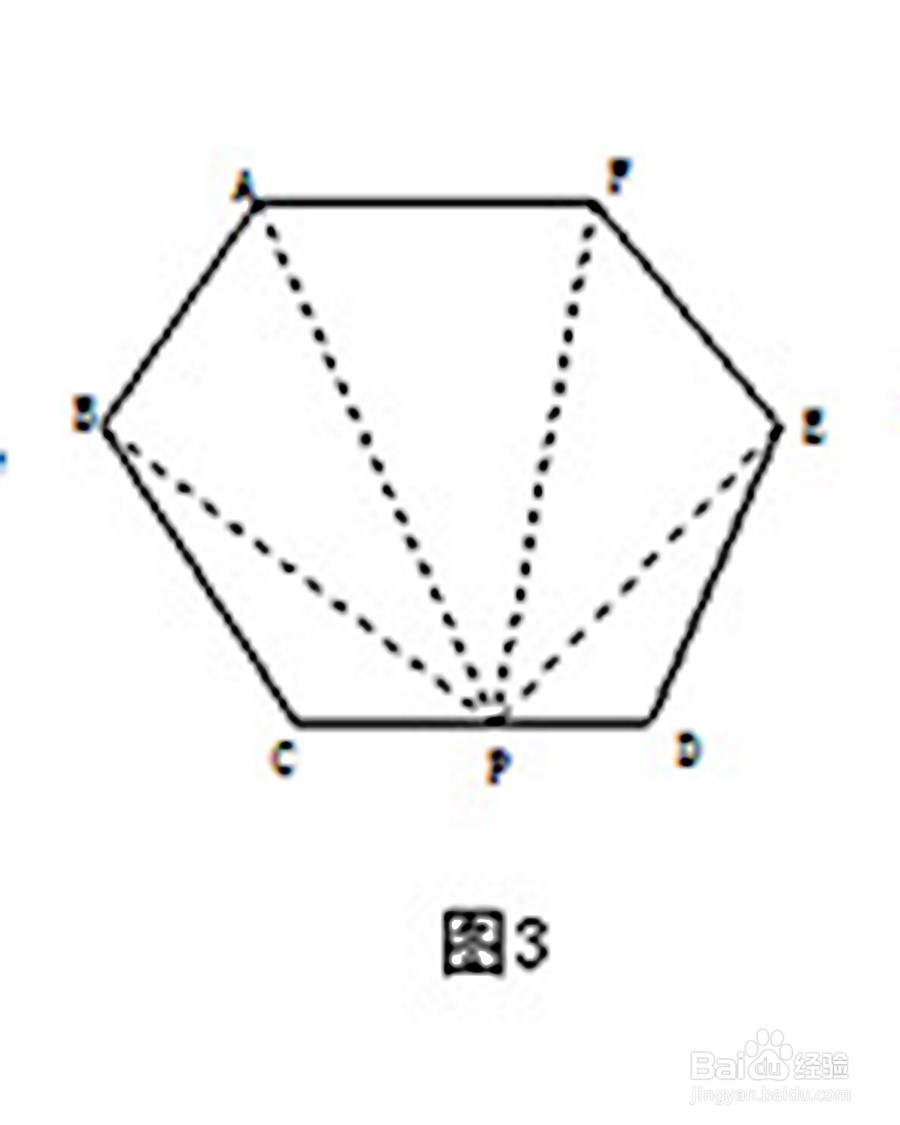
4、方法四:如图4所示,在多边形外取一点P(点P不在n边形任一边的延长线上),连接此点与各顶点,得到五个三角形(不含△CPD),所以此六边形的内角和等于五个三角形的内角和减去△CPD的内角和,即5×180°-180°=4×180°,归纳之后得到n边形的内角和为(n-2)×180°。