1、先来构造这种矩阵的定义:
f[n_] := Module[{A},
A = Table[0, n, n]; (A[[#, # + 1]] = 1) & /@
Range[n - 1]; (A[[# + 1, #]] = 1) & /@ Range[n - 1];
A]

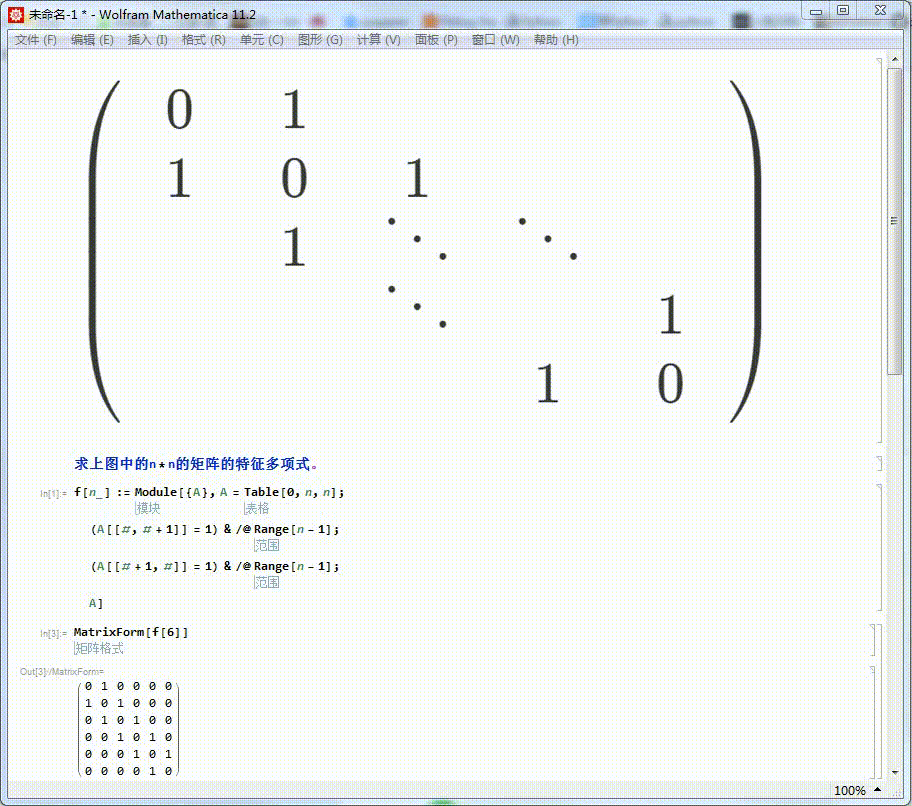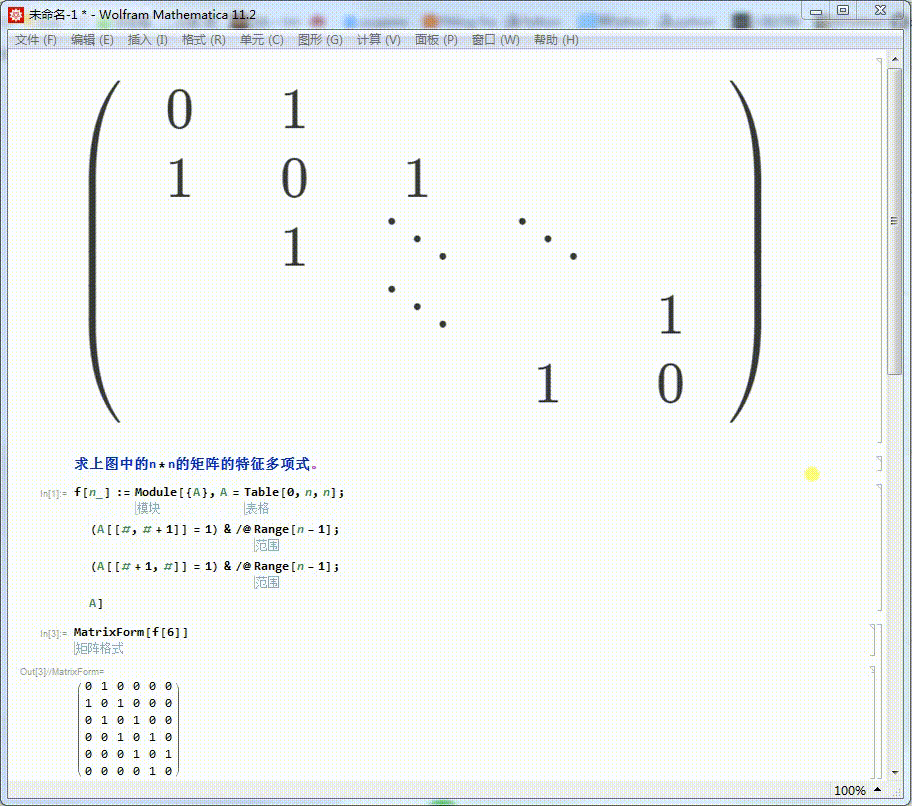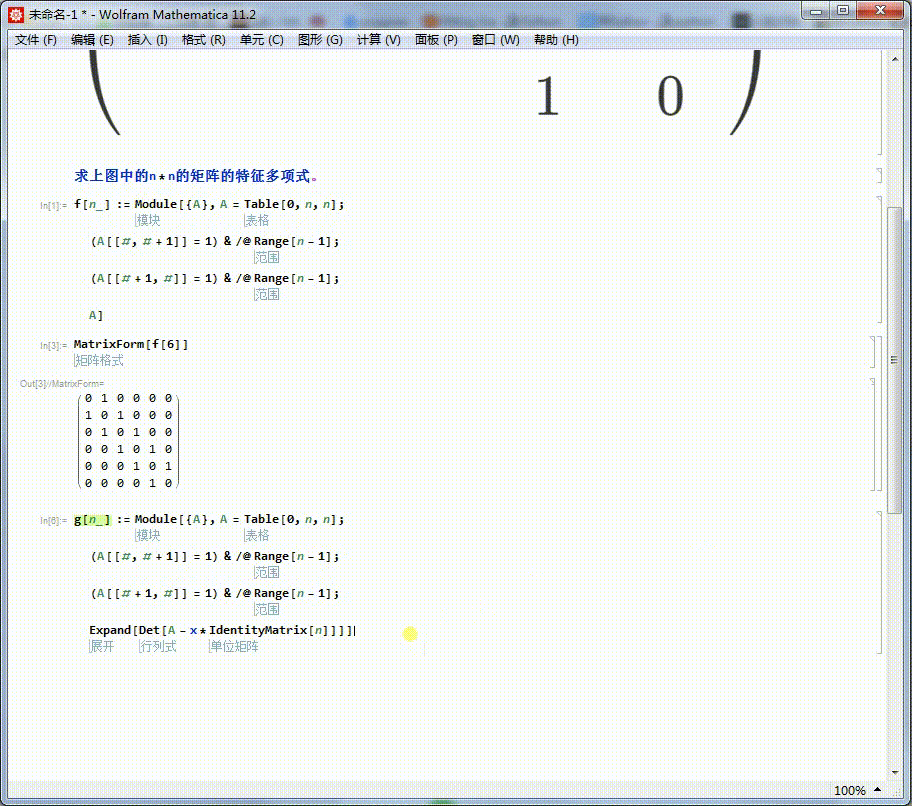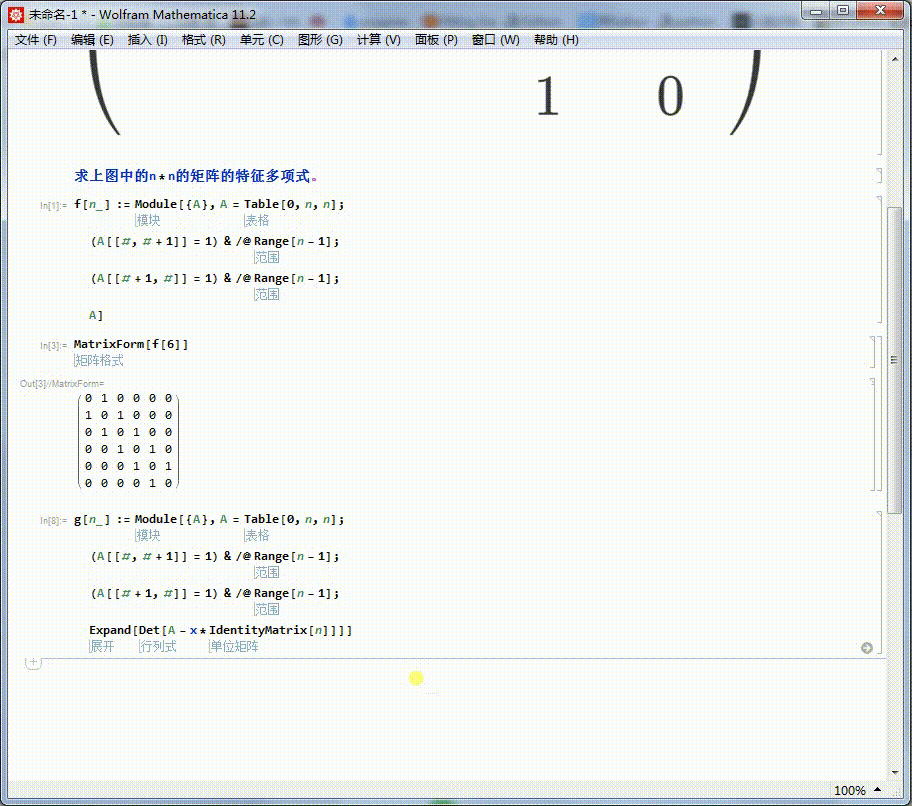
2、我们来看看这种类型的6乘以6的矩阵的模样。
MatrixForm[f[6]]

3、再定义矩阵对应的特征多项式,g[n]。
g[n_] := Module[{A}, A = Table[0, n, n];
(A[[#, # + 1]] = 1) & /@ Range[n - 1];
(A[[# + 1, #]] = 1) & /@ Range[n - 1];
Expand[Det[A - x*IdentityMatrix[n]]]]
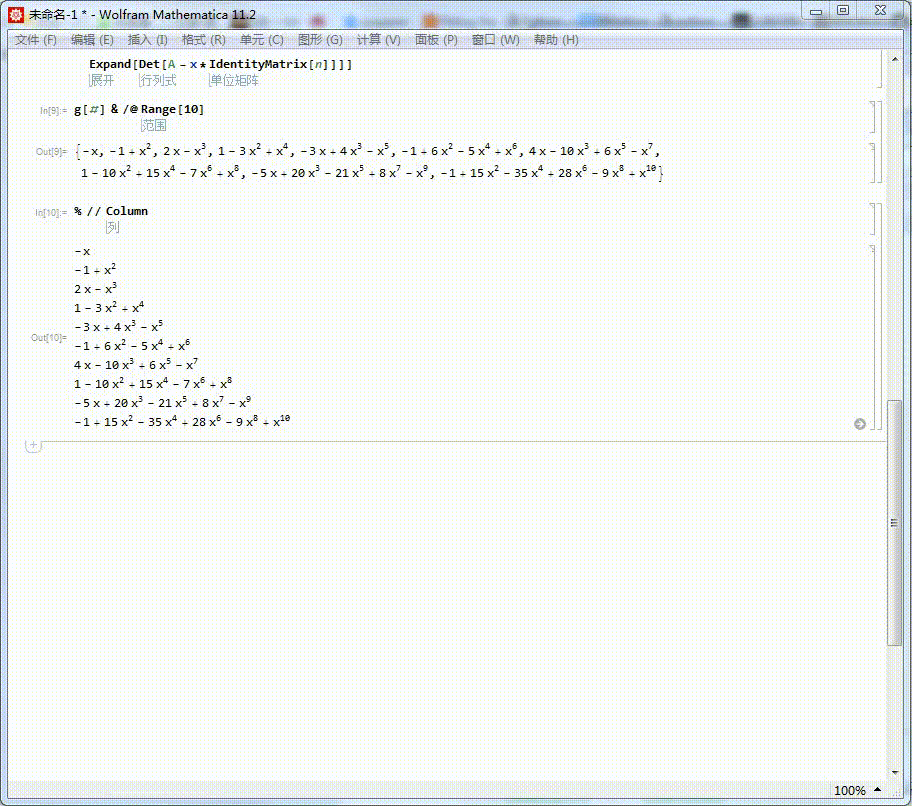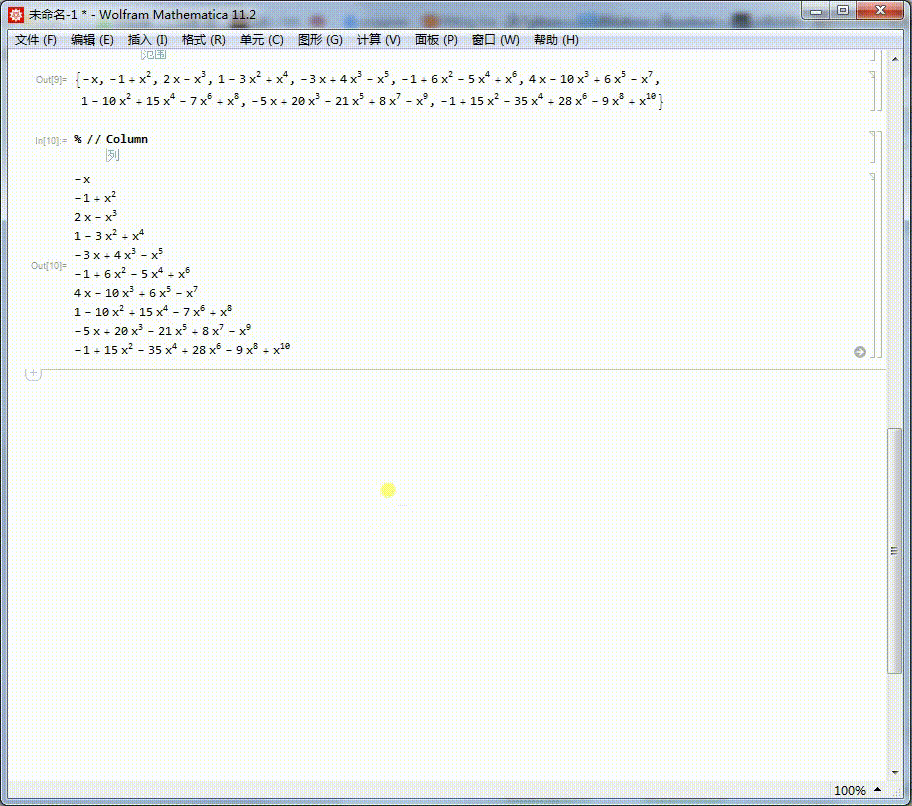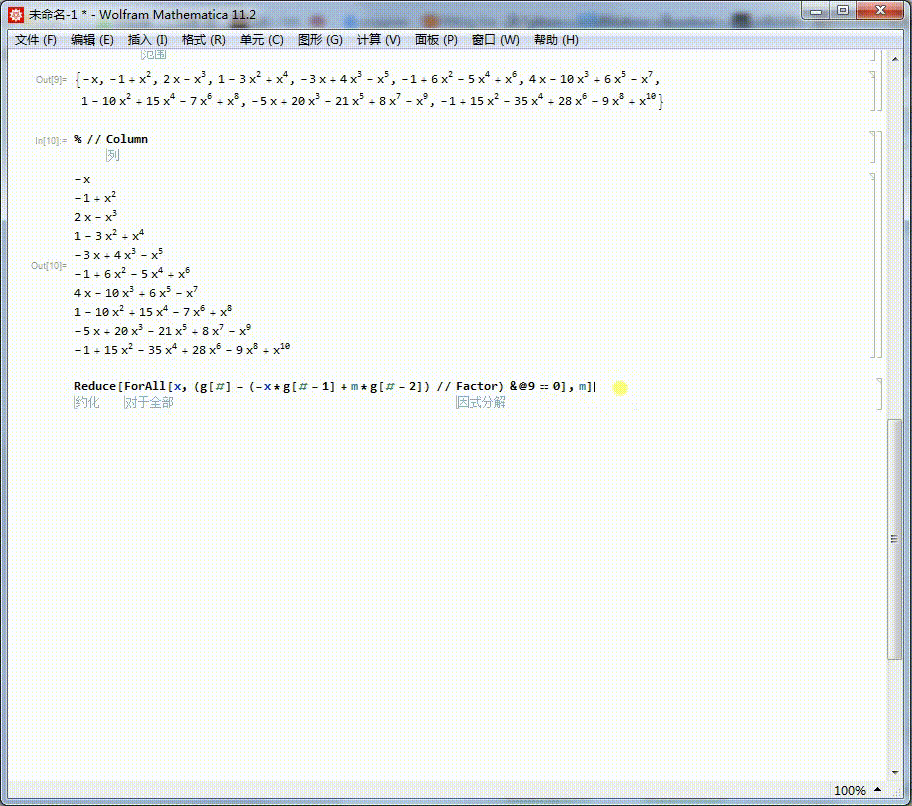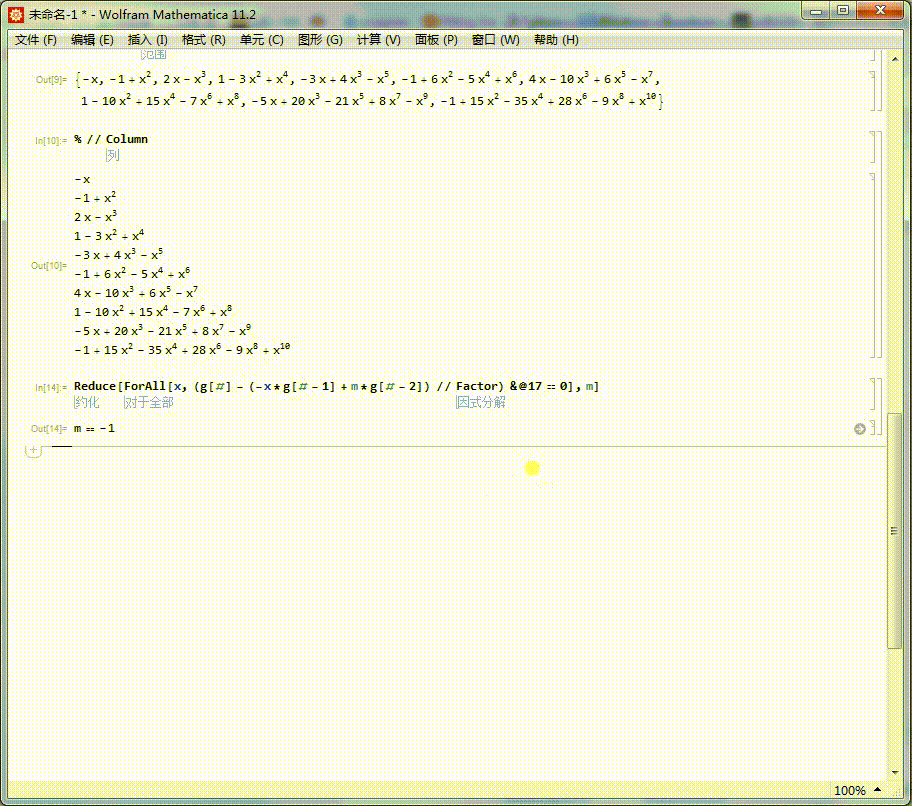
4、查看当n不超过10,所有的这种类型矩阵的特征多项式:
Column[g[#] & /@ Range[10]]
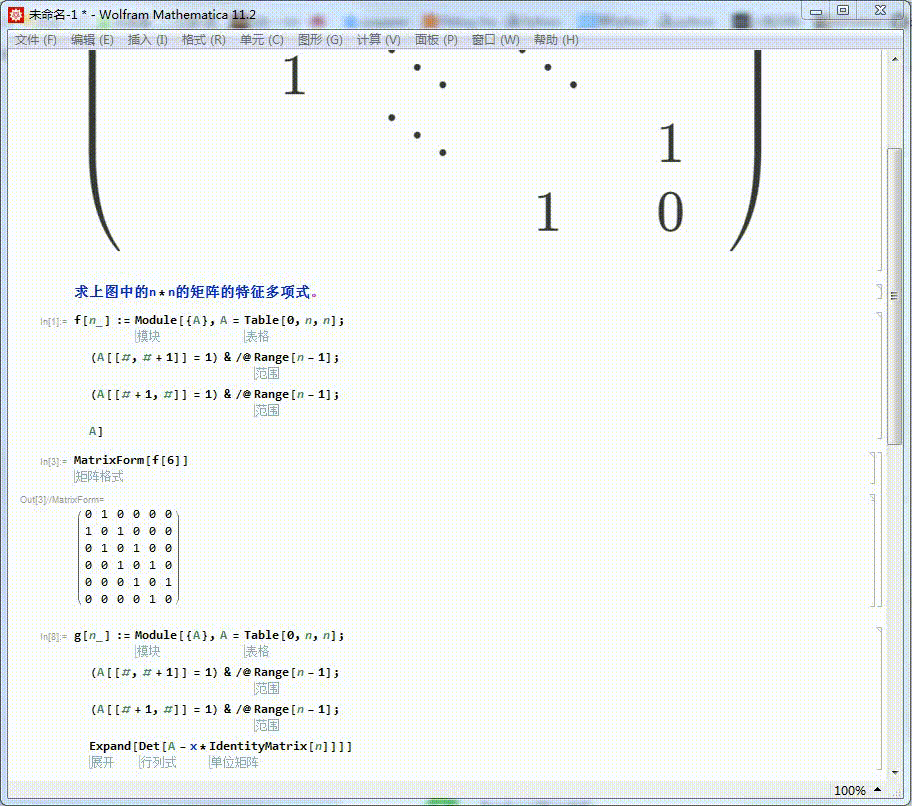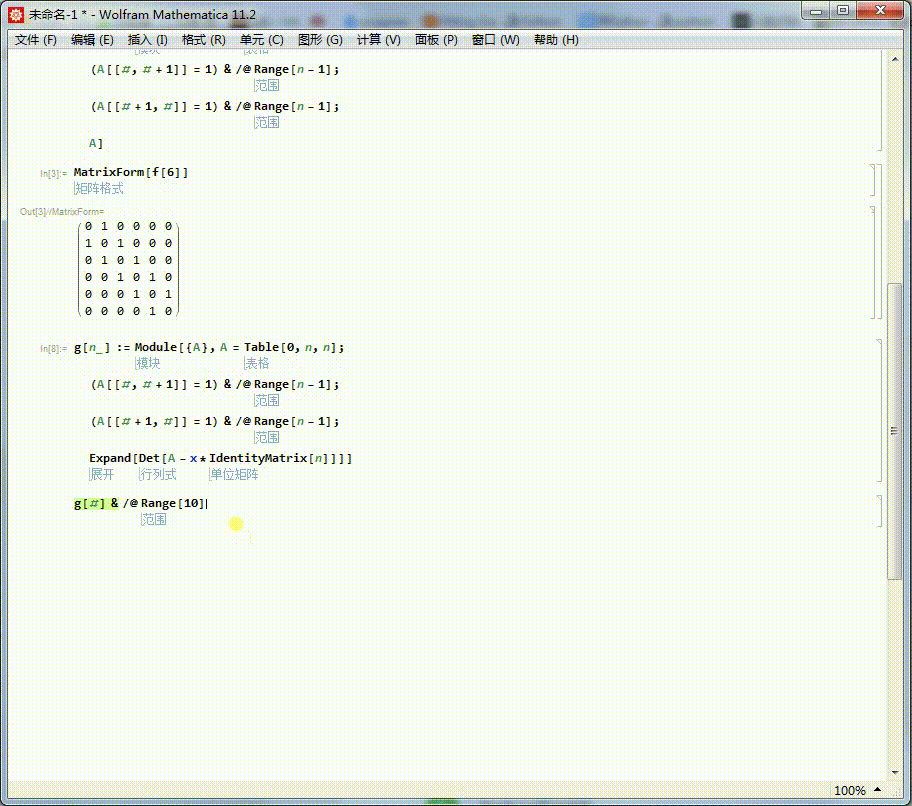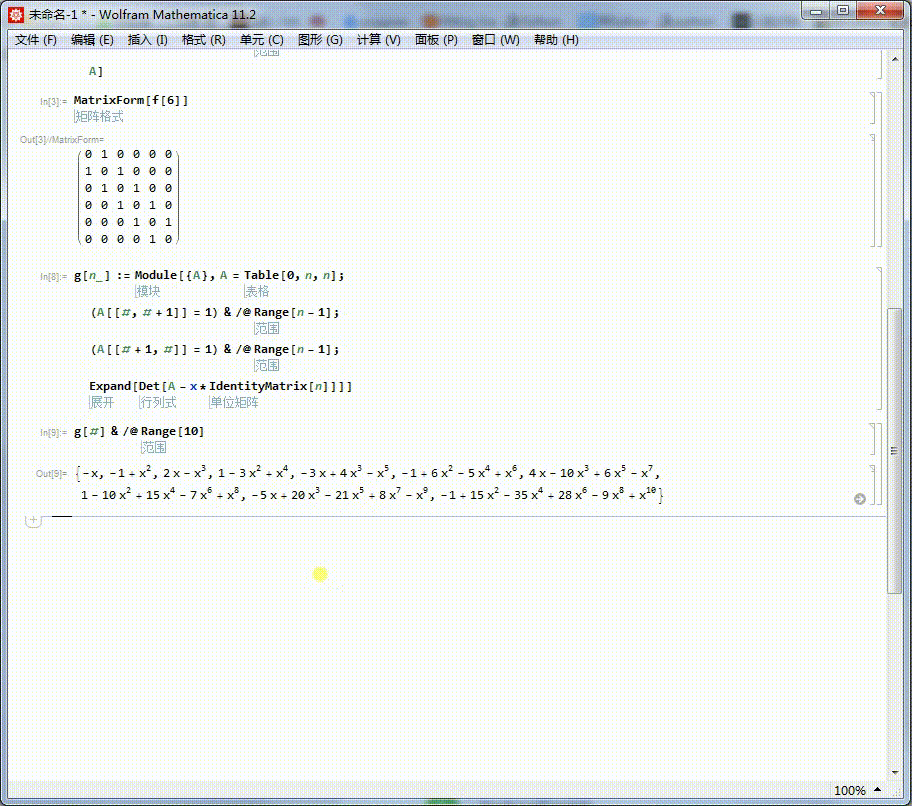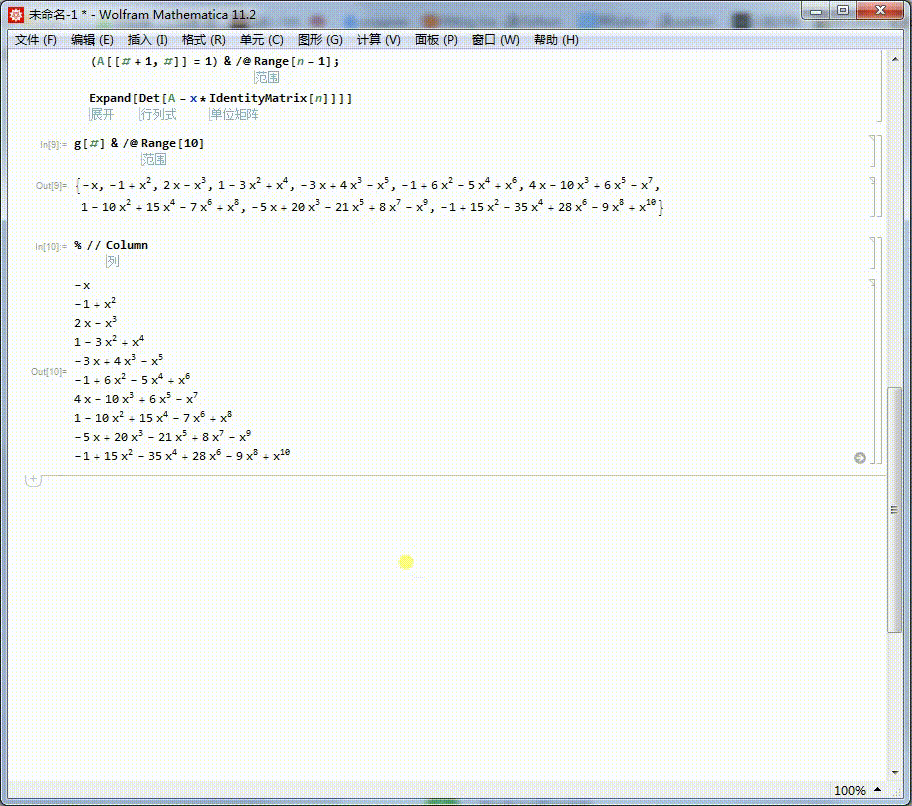
5、但是,这种无止境的枚举法,于此题没有什么益处。我们很难通过这一串式子,观察出多项式的规律。
不过,这些多项式之间存在一种递归规律:
Reduce[ForAll[x,(g[#]-(-x*g[#-1]+m*g[#-2])//Factor)&@9==0],m]
实际上,把9改为任何大于2的正整数,都有m=-1。
6、有了递归公式,初始条件也很容易计算,这样就可以算出通项公式:
RSolve[{a[n + 2] == -x*a[n + 1] - 1 a[n], a[1] == -x,
a[2] == x^2 - 1}, a[n], n] // Flatten // Values
这正是这种n*n类型矩阵的特征多项式。

