有界脑栲葱蛸函数f(x)黎曼可积的充要条件是f(x)几乎处处连续。
作为曲线与坐番舸榆毛标轴所夹面积的黎曼积分对于一在区间[a,b]上之给定非负函数f(x)，我们想要确定f(x)所代表的曲线与X坐标轴所夹图形的面积。
我们可以将此记为黎曼积分的核心思想就是试图通过无限逼近来确定这个积分值。同时请注意，如f(x)取负值，则相应的面积值S亦取负值。
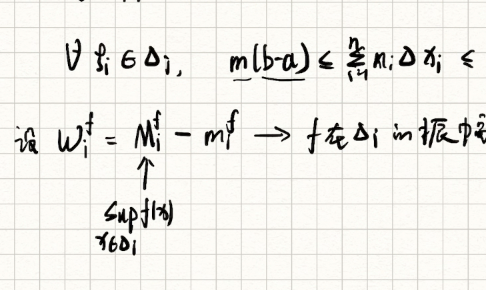
黎曼可积的解释
黎曼积分在应用领域取得了巨大的成功，但是黎曼积分的应用范围因为其定义的局限而受到限制。
勒贝格积分是在勒贝格测度理论的基础上建立起来的，函数可以定义在更一般的点集上，更重要的是它提供了比黎曼积分更广泛有效的收敛定理，因此，勒贝格积分的应用领域更加广泛。
