1、根据函数y=log3(5x^2+3)的特征,即函数y的定义域为全体实数,即定义域为:(-∞,+∞)。

2、求出一阶导数,判断函数的单调性性,并求出函数y=log3(5x^2+3)的单调区间。

3、求函数y=log3(5x^2+3)的二阶导数,判断函数y=log3(5x^2+3)的凸凹性。
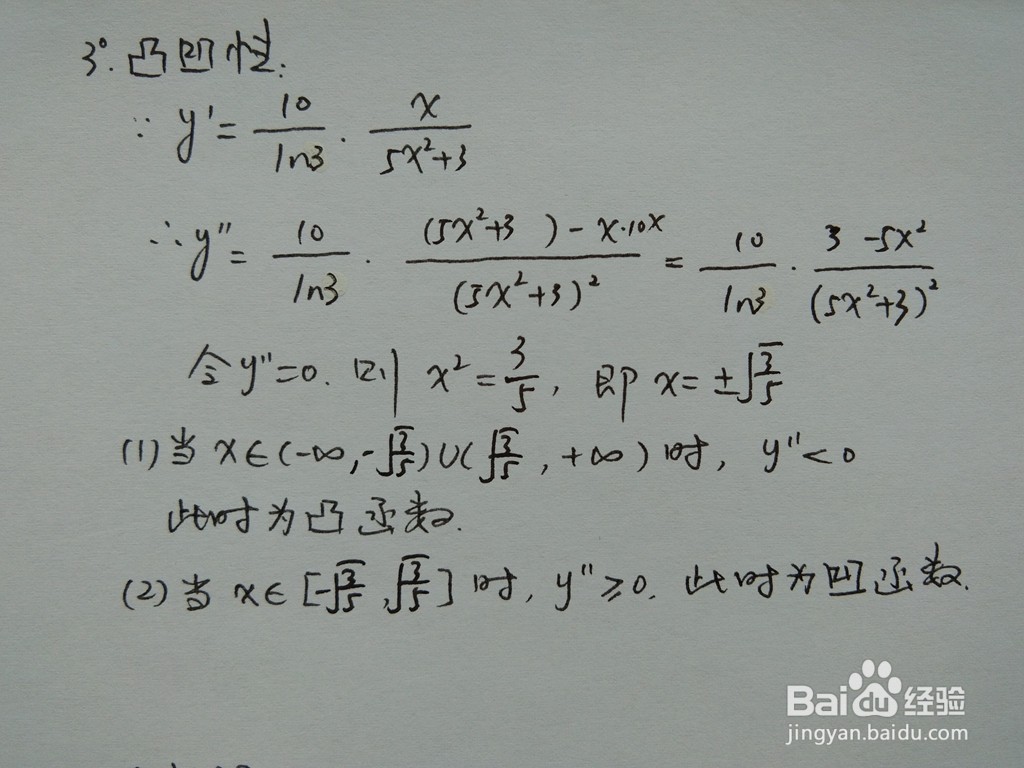
4、函数y=log3(5x^2+3)的极限与奇偶性。

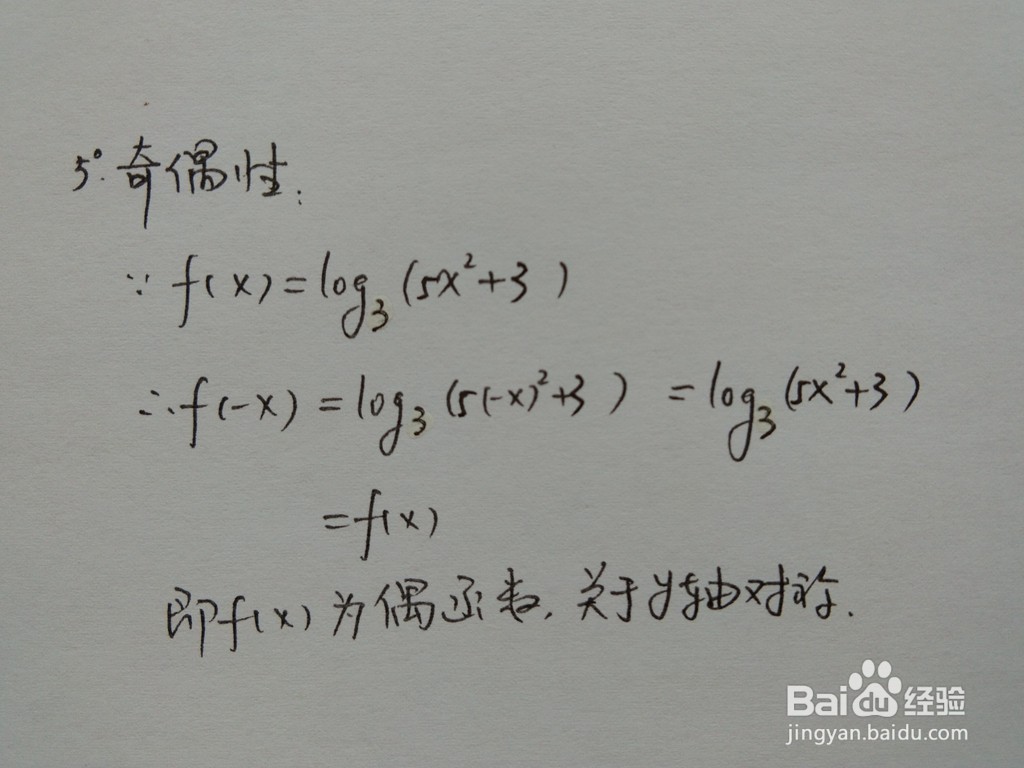
5、该函数y=log3(5x^2+3)的五点示意图。

6、综合以上函数的定义域、单调性、凸凹性,以及函数的极限、奇偶性,简要画出函数y=log3(5x^2+3)的示意图如下。

