1、AB是点A到点C的距离,AC+BC是连接点A、点C的一条曲线长度。
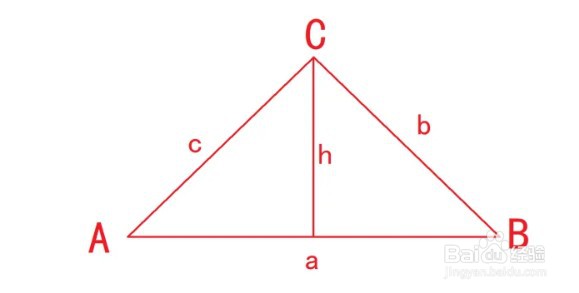
2、根据两点之间线段最短得AC+BC>AB,因此:三角形任意两边之和大于第三边。
3、一、求此三角形的周长C:
C=A+B+C
二、已知此三角形的底边为a,高为h,求此三角形的面积S:
S=ah/2 (面积=底×高÷2。其中,a是三角形的底,h是底所对应的高)注释:三边均可为底,应理解为:三边与之对应的高的积的一半是三角形的面积。这是面积法求线段长度的基础。
时间:2026-02-15 07:09:18
1、AB是点A到点C的距离,AC+BC是连接点A、点C的一条曲线长度。

2、根据两点之间线段最短得AC+BC>AB,因此:三角形任意两边之和大于第三边。
3、一、求此三角形的周长C:
C=A+B+C
二、已知此三角形的底边为a,高为h,求此三角形的面积S:
S=ah/2 (面积=底×高÷2。其中,a是三角形的底,h是底所对应的高)注释:三边均可为底,应理解为:三边与之对应的高的积的一半是三角形的面积。这是面积法求线段长度的基础。
