1、例题:如下图所示,ABCD为正方形,E、F是BC、CD上的点,若角EAF=45度,求证BE+DF=EF.分析:由图可知:要计算两线段相加,若能是两线段在同一条直线上,那么两线段相加,就变成了一条更长一点的线段。问题就变成了证明两条线段相等的问题,证明两线段相等,借助全等三角形的性质即可。以上基本就是截长补短思想在几何中的实际应用。
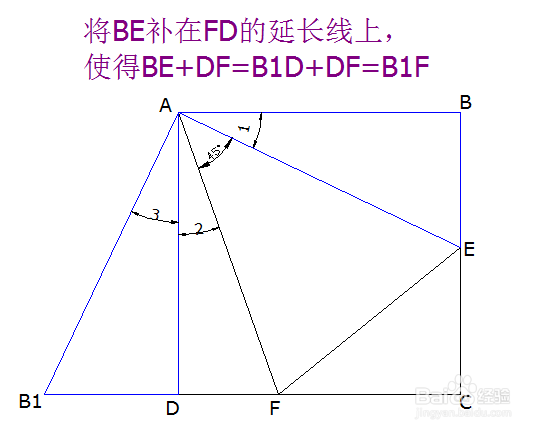
2、第一种补形:用圆规在线段FD的延长线上截取BE长的线段B1D,如下图所示,并连接AB1,即在DF线段上补上一段与BE相等的线段。
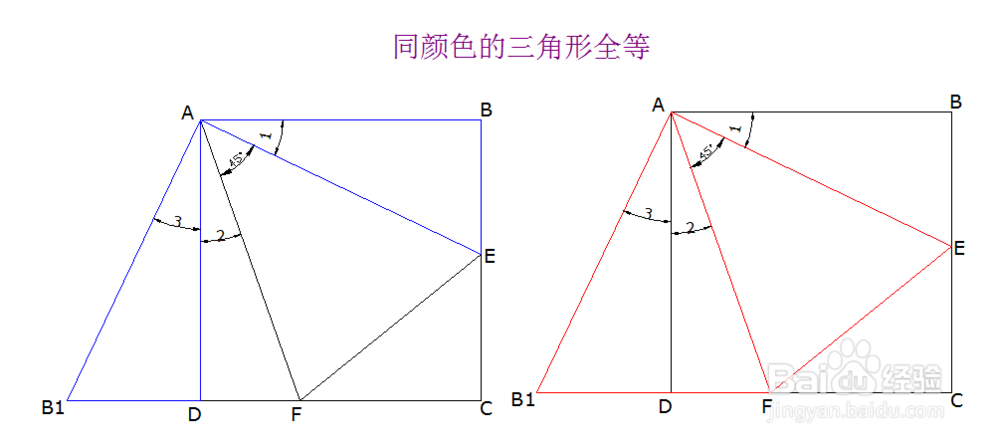
3、具体证明过程如下图所示:其基本思路为,借助两组三角形全等,证明线段B1F=EF,即可证明BE+DF=EF。

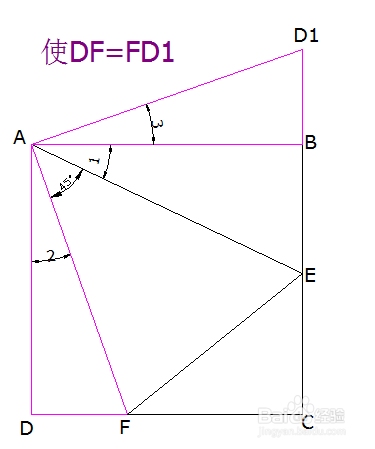
4、第二种补形:用圆规在线段EB的延长线上截取DF长的线段ED1,如下图所示,并连接AD1,即在BE线段上补上一段与DF相等的线段。
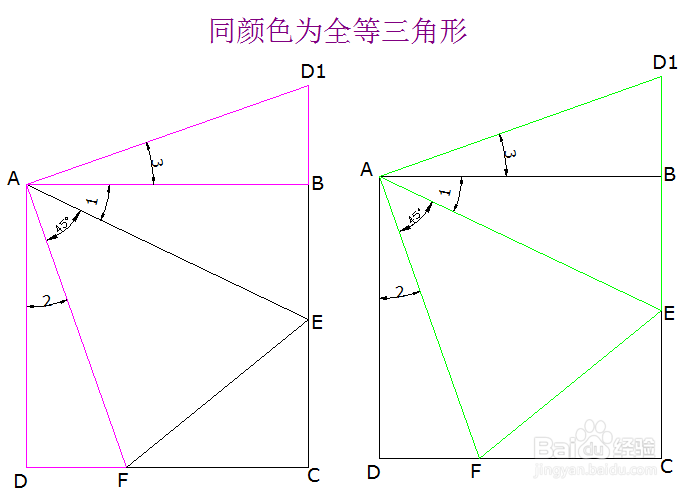
5、具体证明过程如下图所示:其基本思路为,借助两组三角形全等,证明线段ED1=EF,又因为ED1=BE+BD1=BE+DF即可证明BE+DF=EF。

