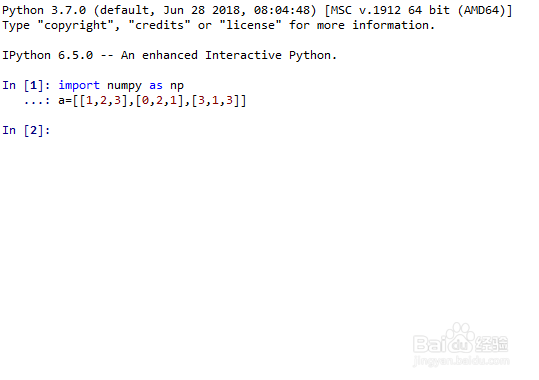
1、给出一个3*3的可逆矩阵:
import numpy as np
a=[[1,2,3],[0,2,1],[3,1,3]]
2、计算a的特征向量:
c=np.linalg.eig(a)
d=c[1]

3、假设d的逆矩阵是d',那么d'.a.d就是一个对角矩阵:
e=np.dot(np.dot(np.linalg.inv(d),a),d)

4、运行结果看起来不是对角矩阵,这是为何?
原来,这是精确度的问题。
如果矩阵中的每个数字都保留两位有效数字,对角矩阵就显出了原形。
e=np.around(e, decimals=2, out=None)

5、矩阵
a=[[1,2,3,3],[0,2,1,2],[3,1,3,1],[3,5,6,9]]
的对角化是:
[[12.56687 0. -0. -0. ]
[ 0. -0.82664 0. 0. ]
[-0. -0. 2.36388 -0. ]
[-0. 0. -0. 0.89589]]

