1、函数y=(x³-1)/(x+1)³是分式函数,躲近诉根据函数特征,分母应不为0。

2、定义域是指该函数的有效范围,函数的沟购定囊帽义域就是使得这个函数关系式有意义的实数的全体构成的集合。
1、通过函数y=(x³-1)/(x+1)³的一阶导数,判断函数的单调性。
2、 函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。

3、导数与函数单调性密切相关。特别是对于具体函数,利用导数求解函数单调性,思路清晰,步骤明确,既快捷又易于掌握。
1、再次计算一阶导数y=(x³-1)/(x+1)³的导数,即通过函数的二阶导数,计算出函数的拐点,进而求出函数的凸凹区间。

2、拐点,又称反曲点,在数学上指改变曲线向上或向下方向的点,直观地说拐点是使切线穿越曲线的点(即连续曲线的凹弧与凸弧的分界点)。若该曲线图形的函数在拐点有二阶导数,则二阶导数在拐点处异号(由正变负或由负变正)或不存在。

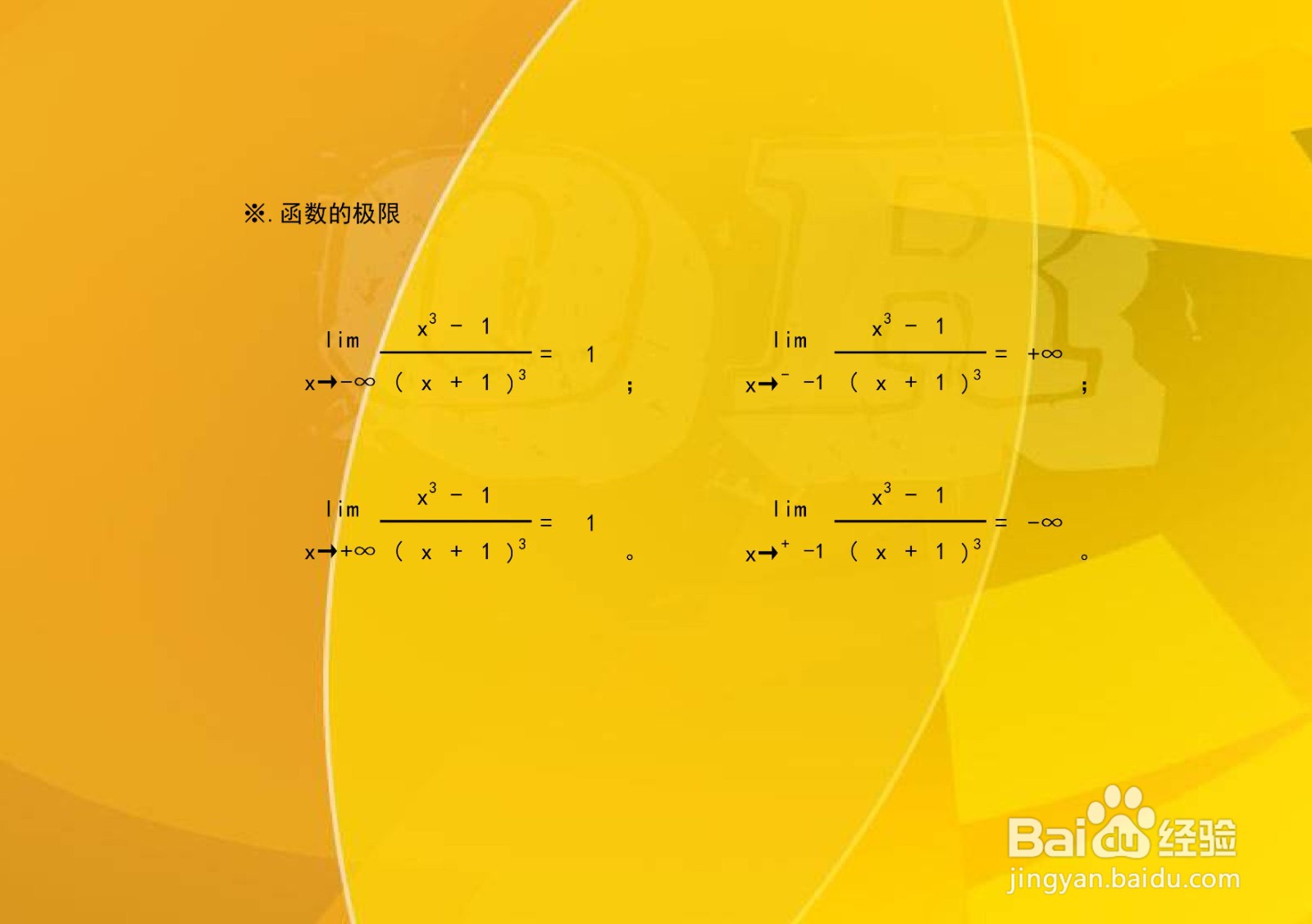
1、判断函数y=(x³-1)/(x+1)³在端点处的极限:
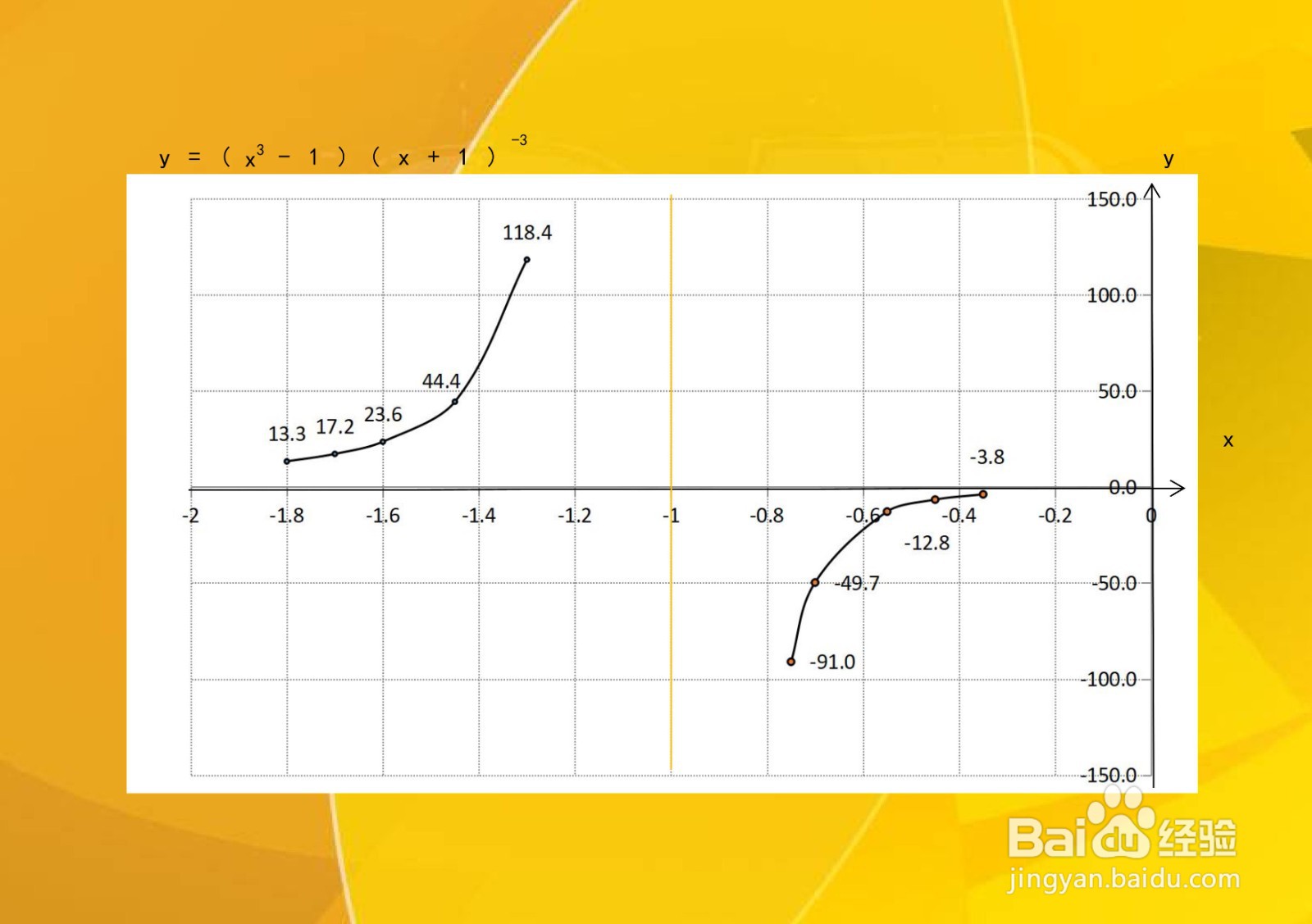
1、根据函数单调性、凸凹性,并结合函数的定义域,列举函数y=(x³-1)/(x+1)³上部分特征点坐标。
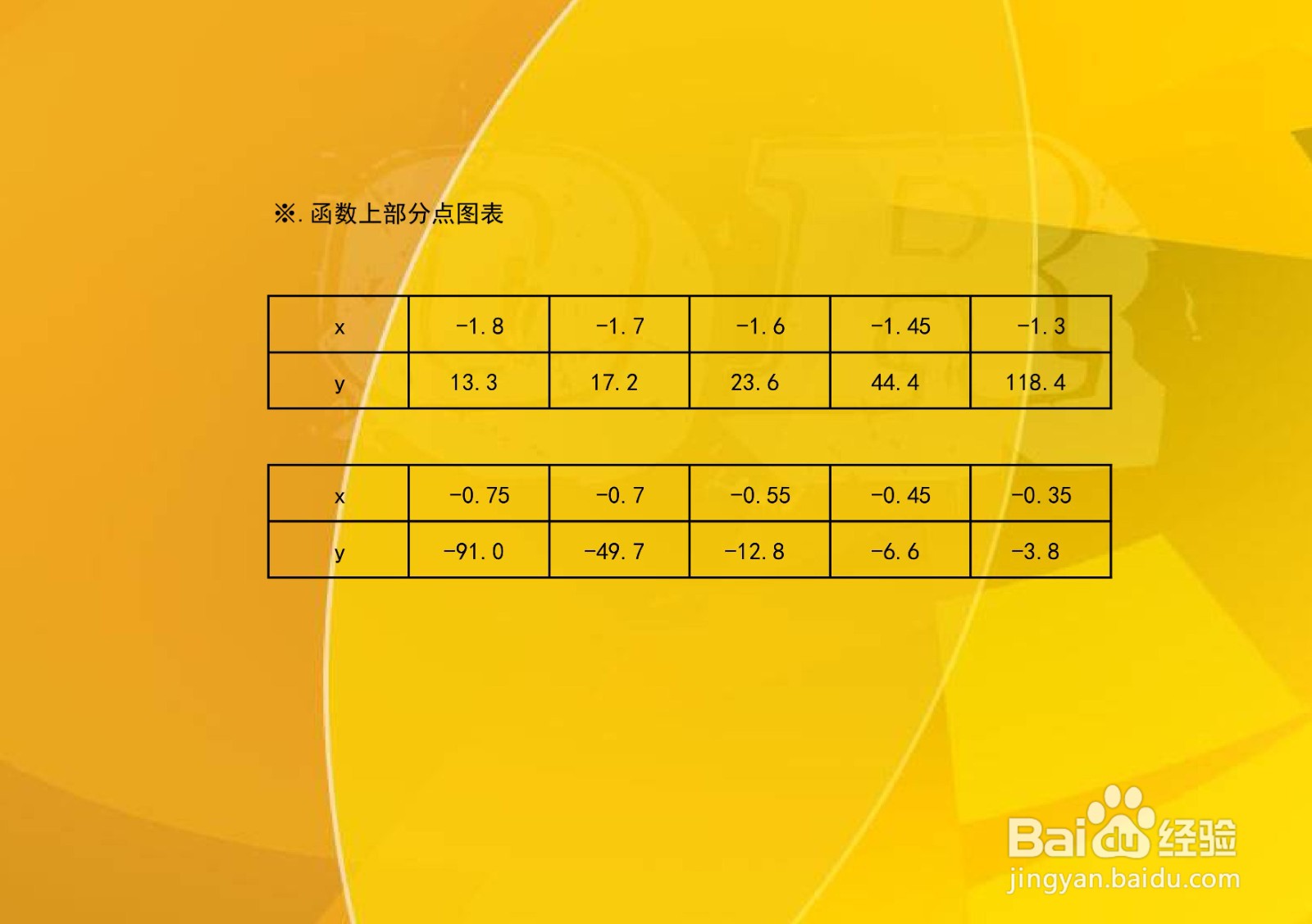
2、综合以上性质,函数y=(x³-1)/(x+1)³的示意图如下: